Про такой сервис, как Shazam, слышали многие — он позволяет, прослушав музыкальный трек всего несколько секунд, практически гарантированно определить его название. С учетом того, что в библиотеке Shazam находится больше миллиона треков, это кажется чем-то из раздела фантастики, однако, очевидно, этому есть научное объяснение, и в этом цикле статей мы и поговорим, как этот сервис работает.

Подписаться на iGuides в Telegram, чтобы узнать обо всем первым — t.me/iguides

Оригинал статьи можно почитать здесь, я лишь ее перевел и несколько адаптировал для более простого понимания. Также я решил разбить эту статью на несколько частей: в начале будет теория — что такое, собственно, звук, как он записывается и что такой аналоговый и цифровой сигналы. В дальнейшем будет введение в оцифровку и описание таких понятий, как квантование и модуляция. Ну и под конец, на основе всего этого, будет объяснено, как же работает сам сервис Shazam. Если вы хорошо знаете физику — теоретические части статьи вы можете пропустить, ну а всем другим — welcome.

Музыка и физика

Звук — это вибрация (вообще говоря — упругая волна, но у нас же научно-популярная статья, верно?), которая может распространяться через любую среду (воздух, воду, даже почву и металлы) и может быть «расшифрована» нашими ушами. Например, когда вы слушаете музыку, наушники (или колонки) производят вибрации, которые распространяются по воздуху до тех пор, пока не достигнут ваших ушей. Свет также является волной, однако мы его не слышим из-за того, что наши уши не приспособлены для его восприятия — однако, к примеру, глаза — приспособлены.

Любая волна может быть с любой точностью аппроксимирована (приближена) совокупностью синусоидальных волн, что здорово упрощает нам жизнь (почему — объясню ниже).

Чистые тона против реальных звуков

Чистый тон — это звук, построенный на гармонических (синусоидальных) колебаниях. Синусоидальная волна характеризуется двумя параметрами:

• Частотой — количеством колебаний в секунду, за единицу измерения принят Герц (Гц). К примеру, 100 Гц = 100 колебаний в секунду.
  
• Амплитудой (связанной с громкостью) — размер каждого колебания (громкость может измеряться в децибелах, но об этом ниже).

Эти характеристики могут быть расшифрованы нашими ушами — к примеру, мы слышим звуки от 20 Гц (низкий гул) до 20 000 Гц (тонкий писк). Разумеется, у всех людей это индивидуально, и обычно к старости верхний порог распознавания звука снижается. Для сравнения, частота волны фиолетового цвета составляет 4 * 10¹⁴ Гц, а красного цвета — 8 * 10¹⁴ Гц, то есть на 10 порядков больше, чем у звуков — именно поэтому мы и не можем слышать цвета ушами.

Вы можете проверить, насколько высокий звук вы можете услышать, с помощью, к примеру, такого ролика на YouTube — однако перед этим проверьте, поддерживают ли ваши наушники и звуковая карта возможность проигрывать высокие частоты вплоть до 20 кГц, ведь в противном случае вы можете наткнуться на предел оборудования, а не ваших ушей.

Наше восприятие громкости зависит от частоты чистого тона. Например, из двух чистых тонов с одинаковой амплитудой, но разной частотой (к примеру, 30 и 1000 Гц), нам будет казаться более громким тот тон, у которого частота выше. Для лучшего понимания этого факта можно почитать Википедию, мы же идем дальше.

На картинке ниже вы можете увидеть чистый тон с частотой в 20 Гц:


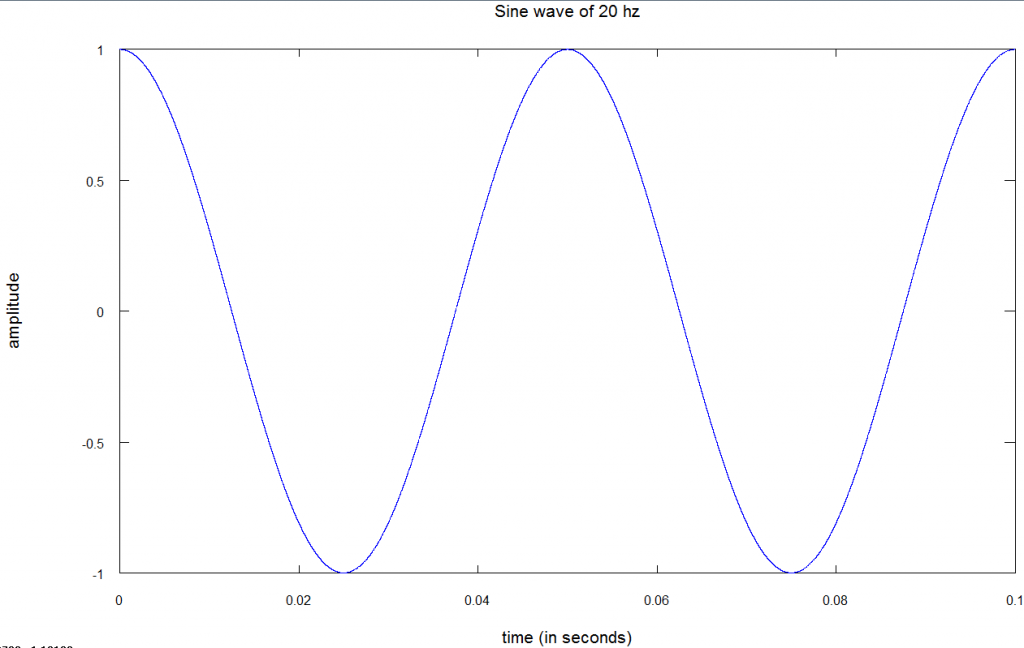
Как я уже писал выше, это — модель, таких волн в природе не существует. Однако любую волну можно разбить на несколько синусоидальных, с разными частотами и амплитудами. Разумеется, это опять же не будет точно соответствовать реальному звуку, но всегда можно добавлять еще волн до тех пор, пока разница не станет незаметной:


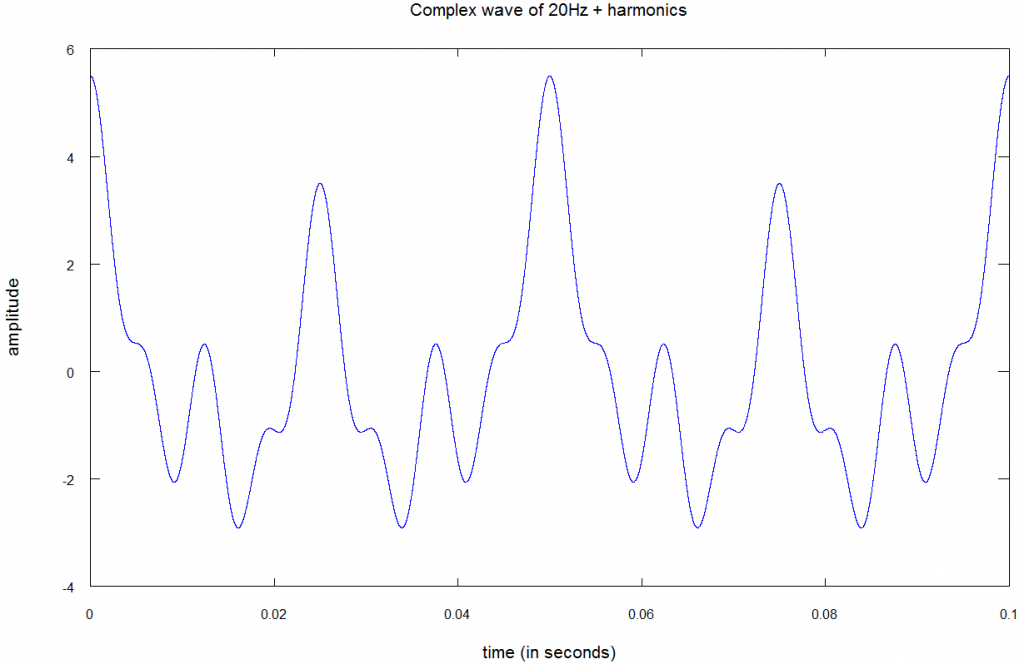
На картинке выше показана волна, уже более приближенная к реальной. В данном случае она состоит из 4-ех синусоид:

• Синусоидальная волна с частотой 20 Гц и амплитудой 1;
• Синусоидальная волна с частотой 40 Гц и амплитудой 2;
• Синусоидальная волна с частотой 80 Гц и амплитудой 1.5;
• Синусоидальная волна с частотой 160 Гц и амплитудой 1.

Разумеется, на практике все существенно хуже, и зачастую реальный звук состоит из тысяч чистых тонов.

Музыкальные ноты

Если вы не учились в музыкальной школе, то сей раздел для вас будет немного трудным. Итак, вот так выглядит нотный стан:
Он представляет собой набор нот, которые расположены на линиях, чем выше — чем больше частота. Также различным типом кружков показывается длительность каждой ноты. В общем и целом — нам нотный стан не понадобится, он здесь просто для наглядности.

Все ноты делятся на октавы — в большинстве стран принято, что в каждой октаве по 7 нот: A, B, C, D, E, F, G (по-русски это Ля, Си, До, Ре, Ми, Фа, Соль). Октава пишется справа от ноты цифрой. Правило получения нот такое — частота одной и той же ноты в каждой следующей октаве удваивается. К примеру, До второй октавы (A2) имеет частоту 110 Гц. До третьей октавы (A3) уже имеет частоту в 220 Гц, 4-ой (A4) — уже 440 Гц. Многие инструменты могут воспроизвести в каждой октаве больше, чем 7 нот — эти «дополнительные» ноты называются полутонами.

Для 4-ой октавы («средняя» октава) ноты имеют следующие частоты:

• C4 (или До3) = 261,63 Гц
• D4 (или Ре3) = 293,67 Гц
• E4 (или Ми3) = 329,63 Гц
• F4 (или Фа3) = 349,23 Гц
• G4 (или Соль3) = 392 Гц
• A4 (или Ля3) = 440 Гц
• B4 (или Си3) = 493,88 Гц

Да, как вы уже поняли, системы обозначения нот в США и в России отличаются, и так как автор текста использует именно американские обозначения — что ж, я тоже буду использовать их в переводе, благо на понимании это никак не отразится.

Забавный момент: у наших ушей логарифмическая чувствительность — а это значит, что и между 32.7 Гц — 61.74 Гц (1-ая октава), и между 261.63 Гц — 466.16 Гц (4-ая октава), и между 2093-3951.07 Гц (7-ая октава) наши уши могут обнаружить одинаковое число нот.

Разумеется, должна быть калибровочная нота, и она есть — это A4 (Ля 3-ей октавы), 440 Гц — именно по ней калибруют акустическое оборудование и музыкальные инструменты.

Тембр

Одна и та же нота звучит по-разному, когда ее играет гитара, фортепиано, скрипка или поет певец. Причина в том, что каждый инструмент имеет собственный тембр для каждой ноты. Создаваемый каждым инструментом звук представляет собой множество частот, которые звучат как данная нота (научный термин — высота звука). Такой звук имеет основную частоту (самую низкую), и несколько обертонов (звуки с частотой, выше основной).

Большинство инструментов производят звуки, близкие к гармоническим — то есть для них обертоны являются кратными основной частоте, и называются гармониками. Например, чистые тона A2, A4 и A6 являются гармоничными (у них разница в частотах в 4 раза между соседними тонами), а вот A2, B3, и F5 — ангармоничны: обычно такие звуки производят ударные инструменты (тарелки или барабаны).

Наш мозг — удивительный прибор: высота звука (воспринимаемая нота) может отсутствовать в звуке, воспроизводимом инструментом. Например, если инструмент издает звук с чистыми тонами A4, A6 и A8, то мозг человека будет интерпретировать его как A2, тогда как самая низкая (основная) частота — это A4. Почитать об этом опять же можно в Википедии.

Спектрограмма

Зачастую песня исполняется сразу несколькими инструментами и певцами. Все эти инструменты создают комбинацию синусоид, а общая картина — еще большая комбинация. При этом ее... можно увидеть — для этого и создана спектрограмма. Она представляет собой трехмерный график, где по горизонтальной оси (X) отложено время, по вертикальной (Y) — частота чистого тона, по третьей оси (Z) — амплитуда волны в определенное время. 

Например, спектрограмма фортепианного воспроизведения ноты C4 (с основной частотой 261.63 Гц), выглядит так:

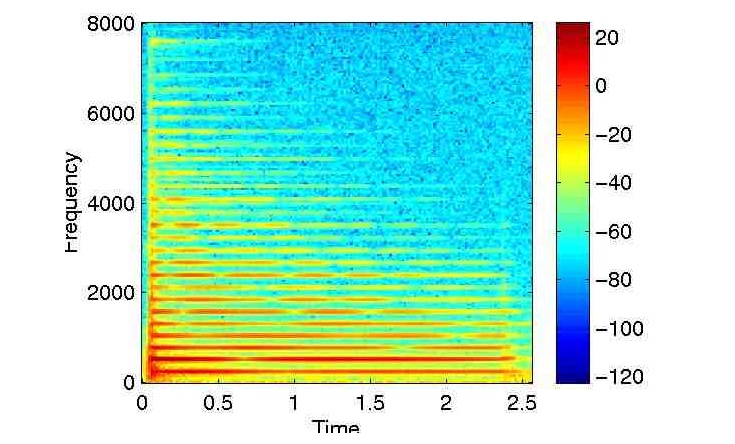
Цветом показана амплитуда волны в дБ (об этом будет дальше). Так как фортепиано является гармоническим инструментом, то в записи явно видны частоты, выше чем 261 Гц у C4.

Еще одним интересным фактом является то, что интенсивность частот меняется во времени — это является особенностью инструмента и делает его уникальным. Поэтому если вы возьмете того же исполнителя, но замените музыкальный инструмент, то звук будет немного другой — с технической точки зрения, меняется огибающая звукового сигнала (которая является частью тембра).

На этом месте уже можно немного поговорить о том, как Shazam «снимает слепок» с композиции — как видно по спектрограмме, некоторые частоты (самые низкие) громче (а значит и важнее) других. Что, если мы будем отсекать все другие, для упрощения работы алгоритма?

Оцифровка

Если вы не любитель слушать музыку с виниловых пластинок, то, значит, вы используете какой-то из цифровых форматов (mp3, ogg, flac). Но вот когда артисты воспроизводят музыку, она аналоговая — то есть не представлена битами. И чтобы хранить такую музыку и воспроизводить на электронных устройствах, она оцифровывается — и о том, как это делается, мы поговорим ниже.

Дискретизация

Аналоговые сигналы являются непрерывными, то есть вы можете бесконечно уменьшать промежуток звучания сигнала, и вы каждый раз будете получать разный звук. Однако в цифровом мире мы не можем хранить бесконечное количество информации, поэтому тут приходится идти на хитрость и задавать минимальную единицу звучания — к примеру, 1 миллисекунду: в этот промежуток времени звук не может меняться. И это время уже гибко настраивается так, чтобы, с одной стороны, цифровая песня звучала как аналоговая, но, с другой стороны, так, чтобы трек весил не очень много. Представьте, к примеру, что в вашей любимой песне звук меняется только раз в пару секунд (технический термин — сглаженный звук). Узнаете ли вы ее? Вряд ли. С другой стороны, можно сделать это время в 1 наносекунду (10^-9 с) — тогда качество будет отличным, но вот вес трека, увы, не порадует. За эту проблему поиска оптимальной единицы времени и отвечает дискретизация.

Стандартная дискретизация в цифровой музыке — это 44 100 единиц (выборок) в секунду. Откуда взялись эти 44.1 кГц? Ну, какой-то человек подумал, что число 44 100 отлично подходит, и все заверте... Шучу, конечно же нет.

Как мы помним, люди могут слышать звуки от 20 Гц до 20 кГц. В теореме Котельникова, она же теорема Найквиста-Шеннона (давайте я не буду ее приводить дословно, ладно?) говорится, что если вы хотите оцифровать сигнал от 0 до 20000 Гц, то вам потребуется не менее 40000 выборок в секунду. Основная идея тут в том, что синусоидальный сигнал на частоте F нуждается в определении не менее 2 точек за цикл, и, если частота вашей дискретизации не меньше, чем частота вашего сигнала, вы получите как минимум 2 точки за цикл исходного сигнала.

Попробуем понять это на примере. На картинке ниже звук с частотой в 20 Гц оцифровывается с частотой дискретизации в 40 Гц:

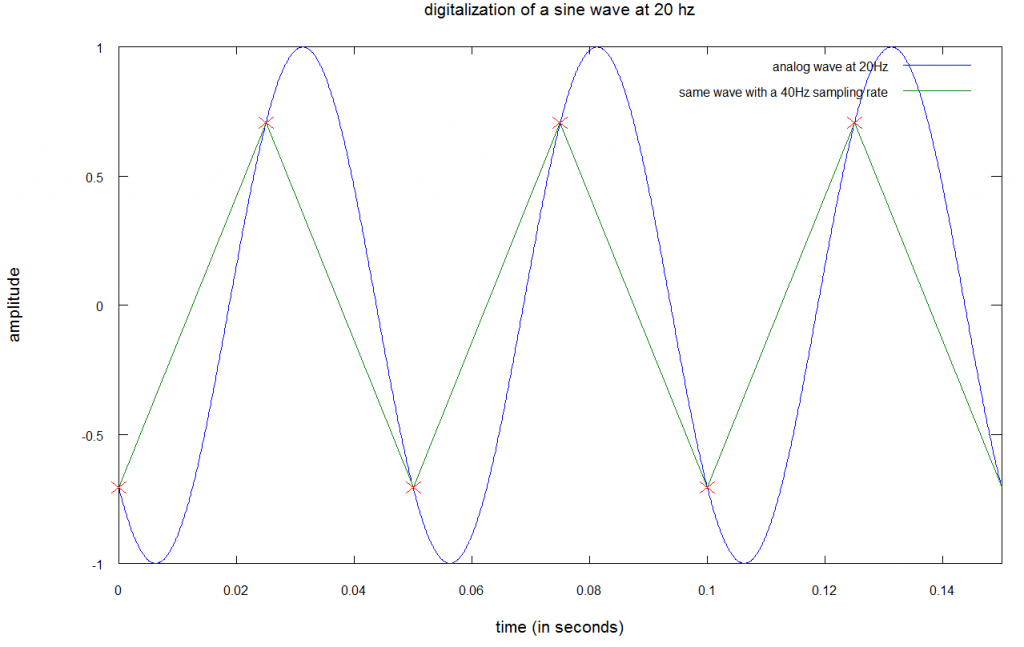
Синяя кривая представляет себе исходный синусоидальный сигнал с частотой в 20 Гц. Красные кресты — это наша выборка, дважды за цикл. Зеленая линия — интерполяция (приближение) исходного звука. Вы скажете — что-то не похоже это на наш звук. Так и есть, обычно частота дискретизации выше эдак на 3 порядка. 

Чтобы было еще понятнее — ниже пример плохой выборки, когда звук с частотой в 20 Гц оцифровывается с частотой дискретизации в 30 Гц:


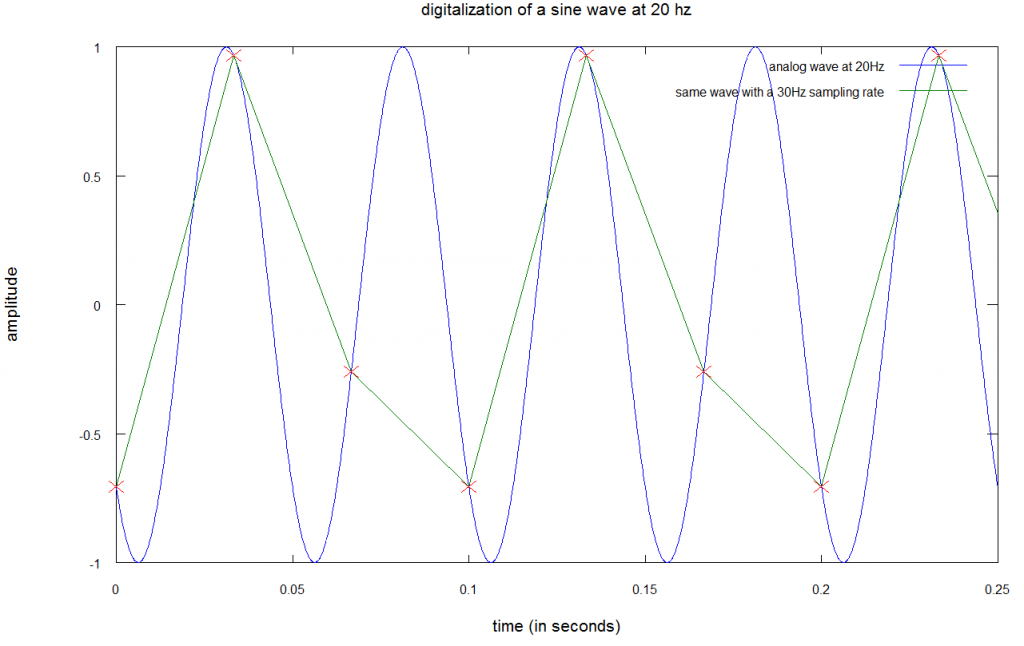
Тут, как видно, частота дискретизированного сигнала не совпадает с исходным сигналом — разница между ними в 10 Гц. И, если присмотритесь, то увидите, что один цикл в дисктеризированном сигнале представляет два цикла в исходном сигнале — это называется подвыборкой.

Также этот случай показывает кое-что еще: если вы хотите оцифровать сигнал между 0 Гц и 20 кГц, то вам необходимо перед этим убрать из него все частоты выше 20 кГц и ниже 0 Гц — в противном случае, эти частоты преобразуются в частоты между 0-20000 Гц и, следовательно, добавят нежелательные звуки (это называется наложением спектров).

Подводя итог: если вы хотите качественное преобразование аналоговой музыки в цифровую, то вы должны записывать ее с выборкой не менее 40000 единиц в секунду. HIFI-корпорации (например, Sony) выбрали частоту в 44.1 кГц еще в 80-ых, потому что она была выше необходимых 40 кГц и совместима с форматами NTSC и PAL. Существуют и другие стандарты — к примеру, 48 кГц (Blueray), 96 и 192 кГц, но, если вы не профессионал и не аудиофил, то, скорее всего, вы слушаете музыку в 44.1 кГц.

На этом мы, пожалуй, закончим сегодняшнюю часть статьи. В следующей части будет квантование, модуляция и дискретное преобразование Фурье (не пугайтесь — там не будет ничего сложного). Ну а после этого мы уже будем готовы посмотреть, как именно работает Shazam.