
Теория хаоса утверждает, что незначительное событие или обстоятельство может иметь огромное влияние на формирование пути развития большой и сложной системы в будущем. Многие знакомы с этим так называемый «эффектом бабочки» по рассказу писателя-фантаста Рэя Брэдбери 1952 года «Звук грома». В нем человек, который отправился в глубокое прошлое, чтобы поохотиться на тираннозавра, случайно раздавил своей ногой бабочку. Когда он возвращается в настоящее, то обнаруживает, что этот, казалось бы, незначительный акт изменил ход истории — и не в лучшую сторону.
В начале 1970-х годов метеоролог и математик Эдвард Нортон Лоренц сформулировал эффект бабочки в науке и положил начало теории хаоса. Говоря простым языком, эта теория гласит, что начальные условия сильно влияют на эволюцию очень сложных систем. По метафоре Лоренца, взмах крыльев бабочки в Бразилии может в конечном итоге привести к торнадо в Техасе, которое в противном случае не произошло бы. Подразумевается, что если бы мы могли вернуться назад и хотя бы немного изменить прошлое, внутри системы возникло бы другое будущее. При этом будущее, содержащее наше настоящее, исчезнет.
Эффект бабочки хорошо работает в нашем повседневном мире, где классическая физика описывает системы выше атомного масштаба. Но в субатомном мире, где царит квантовая механика, действуют другие — и очень странные — законы и правила. Сохраняется ли там эффект бабочки? И если нет, что происходит вместо него?
Бин Ян и Николай Синицын в своей статье в журнале Physical Review Letters исследовали этот аспект квантовой механики, когда разрабатывали новый метод защиты квантовой информации. Используя свойство квантовой запутанности, когда состояния двух связанных кубитов (квантовых битов) зависят друг от друга, они искали способ сделать их невосприимчивыми к повреждениям. Тогда такие кубиты можно будет полностью восстановить, даже если кто-то попытается повредить или украсть информацию. Эта способность поможет защитить квантовую информацию, а также предоставит способ скрытия данных.
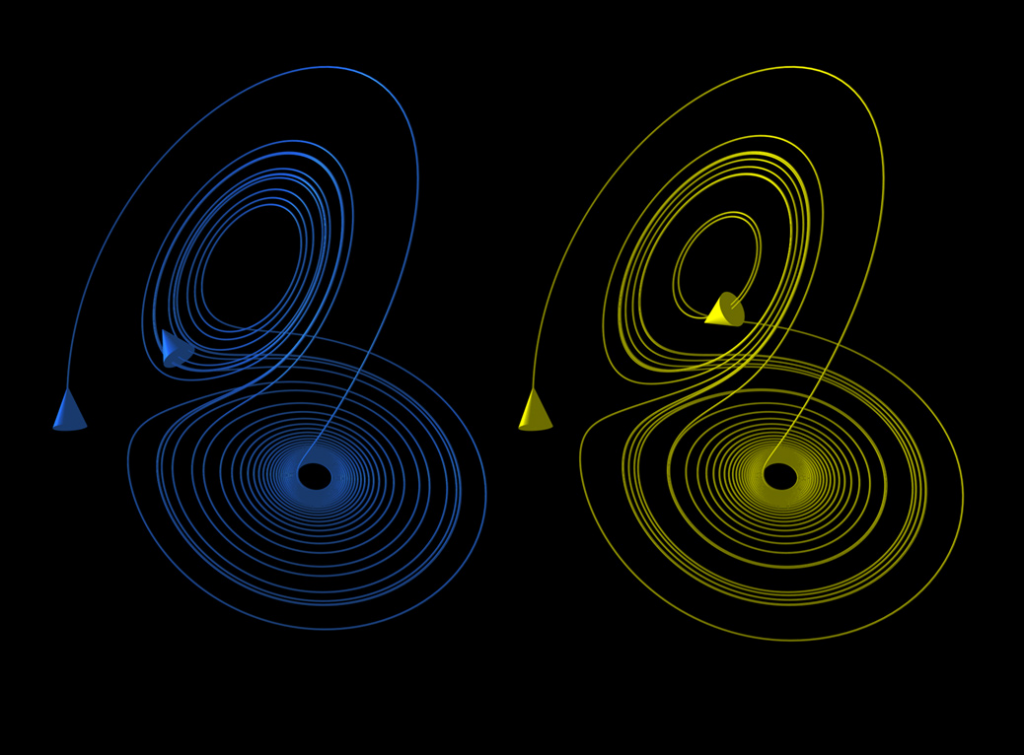
Демонстрация эффекта бабочки: начальные параметры обоих объектов отличались лишь на 0.01%.
Ученые ожидали получить в квантовом мире эффект бабочки, схожий с нашим макромиром. Это выглядит разумно: когда квантовая система развивается в течение длительного времени, локальные переменные, описывающие конкретный кубит в некогда двойниковых запутанных системах, в конечном итоге будут иметь очень разные значения — другими словами, сработает эффект бабочки.
В своем мысленном эксперименте Ян и Синицин привлекли старых друзей каждого квантового теоретика, Алису и Боба. Система, которую они рассматривали, сложным образом развивалась в зависимости от времени, то есть, по сути, двигалась в обе стороны во времени. Итак, в начале Алиса «записывает» информацию на кубит в настоящем и запускает систему в обратном направлении, имитируя путешествие в прошлое. В прошлом Боб «считывает» информацию, хранящуюся в кубите Алисы. Поскольку получение информации о кубите в квантовом мире изменяет его состояние, оно меняет и саму информацию. Кроме того, по законам квантовой динамики такое получение информации разрушает все квантовые связи этого кубита с остальными квантовыми битами.
Поэтому логично предположить, что если запустить систему после такого путешествия в прошлое заново, то настоящее, в котором Алиса записывает информацию на кубит и отправляет его в прошлое Бобу, должно существенно измениться. Это будет означать, что Алиса не сможет восстановить свою информацию после наступления «нового настоящего».
Но этого не произошло.
Для проверки мысленного эксперимента Ян и Синицин решили смоделировать его на реальном квантовом процессоре IBM-Q. Для моделирования путешествия во времени ученые проводили логические операции над запутанными кубитами в прямом и обратном порядке. В начале они таким образом отправили все кубиты «в прошлое», проведя над ними цепочку логических операций, далее они измерили состояние одного кубита, тем самым разрушив его запутанность, и после этого вернули кубиты «в настоящее», проведя те же операции в обратном порядке.

Квантовый компьютер IBM-Q, работающий с 20 кубитами.
Результат оказался удивительным: измеренный кубит вернулся практически в то же состояние, в котором находился до начала эксперимента, плюс небольшой фоновый шум. То есть из-за того, что начальное состояние всей системы было сильно запутано, долгие сложные логические операции в обратном порядке восстановили потерянную информацию об измеренном кубите.
Таким образом, к своему собственному удивлению, Ян и Синицын не только опровергли эффект бабочки в квантовой системе, но и также обнаружили своего рода эффект отсутствия бабочки, как будто система хочет защитить настоящее.
Сильная запутанность в квантовом смысле означает, что система изначально имела устойчивые квантовые зависимости между своими частями. То есть запутанные кубиты хоть и обладают разными свойствами, в некотором смысле они действуют как одно целое. В итоге даже после изменения локальной информации квантовые взаимосвязи между всеми запутанными кубитами ставят своего рода защиту на квантовую динамику системы, заставляя ее восстанавливать поврежденные локальные переменные. И чем сложнее запутанная система, тем больше квантовых взаимосвязей она порождает и тем надежнее «защищает настоящее».
К слову, этот результат «отсутствия бабочки» уже имеет практическое применение, например, для проверки квантовых компьютеров. Там, где неясно, действительно ли квантовый компьютер использует квантовую механику для получения результатов — он все еще может полагаться на классическую физику — для проверки можно использовать эффект отсутствия бабочки, потому что он является чисто квантово-механическим. Еще одно потенциальное применение — это защита информации, поскольку случайная эволюция квантовой системы защитит данные при атаке, изменяющей состояния некоторых кубитов в ней.
В дальнейшем Ян и Синицын планируют экспериментально проверить эффект на реальной физической квантовой системе в лаборатории (а не на квантовом компьютере), вероятно, с использованием ультрахолодных атомов, которые ведут себя квантово-механически. Это позволит продемонстрировать эффект в условиях, которые могут быть применены к практической проблеме защиты квантовой информации.
Помимо этих практических применений, эффект отсутствия бабочки поднимает интересные вопросы о различиях между квантовой сферой и миром классической физики, в котором мы в основном живем. Большинство физиков считают, что квантовая механика применима к масштабам, который мы уже можем наблюдать, и она действительно часто дает те же предсказания, что и классическая физика.
Однако физики все еще пытаются понять, как классический мир возникает из квантового в нашей повседневной жизни. Вопрос о том, в какой степени эффект бабочки может применяться в привычном нами макроскопическом мире, остается открытым, как и степень, в которой классический эффект бабочки может применяться в квантовом мире. Ученые надеются ответить на эти вопросы в будущих исследованиях.











